Scribe Post 9/10

We began class by taking a 40 minute quiz. After the quiz, we read through Francie's scribe post from last class. After that Mr. O'Brien put a warm up on the board in which we were instructed to find three limits.  The three equations are:

a.)

b.)

c.)

The class took a shot in the dark, and Mr. O'Brien stated that there were errors, only to realize he was in fact the culprit. Cooper scrawls a messy answer but Mr. O'Brien still insists the answers aren't perfect. While the class continued to solve the Warm-Up, we reviewed Francie's scribe post. Connor, with eyes like a hawk, spots a slight error in Francie's work. Together, the class watched a math related clip from one of the great classic films of our time, Mean Girls.

Turning back to the problems at hand, all the examples on the board are examples of indeterminate form. This is when you get 0/0 when using substitution.  When dealing with indeterminate form you cannot just substitute.  Note that this is different that the problem we earlier dealt with, , which can be rewritten as  . While the denominator would be 0 if we substituted 2 directly in for x, we avoided this by realizing we could factor first, which allows us to cancel out the (x-2)'s.  While this problem potentially gives a denominator of 0 when substituting, factoring avoids this.  We are left with (x+3), where 2 can be substituted in to give us a limit of 5.  Note that the three warm-up problems won't work this way since they are indeterminate form.

So really, what is the indeterminate form? 

The indeterminate form technically gives you an answer of anything since you are not just dividing by zero, but you have 0/0, which gives a possibility of anything.  Using an explanation on Khan Academy, we see that undefined means there is no possible value, while indeterminate means there could be any value and there is not enough information given.  This is explained in this video.

This is shown in warm-up b, , where you can factor out an x and then cancel to get , which, using substitution of 0 for x, since , gives us 1/0.  This is undefined as opposed to indeterminate.  1/0 is infinitely large, which is a non-existant limit.  The goal by the end of the day was to answer the first 3 warm-up problems without using a calculator.  To do this, we need to first know the sandwich theorem, which will help us solve problem a.  In an example, , we can let .  As x approaches 0, theta approaches 0 as well.  You can sub a 3 into the numerator and denominator and you get . We know that .  This is the same problem as a, which was but with x instead of theta.  Since the answer to a is 1 (which we know by using a calculator) , we can sub into to get 3 times 1, which is equal to 3.

Algebraically solving problem c, which is , if we substitute immediately we get we can use a FUFOO, or in this case, as Cooper expertly points out,.  Multiplying that FUFOO by c, we get , which simplifies to .  Then we can use sin rules to get 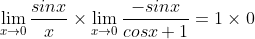.  This can be confirmed using a calculator.  Cooper triumphantly shouts "hell yeah" as he understands the concept. O'Brien points out that using a calculator on indeterminate form will always work.

Cooper asks how the limit of problem a = 1 algebraically. This excites O'Brien greatly, seeing as this is the entire key to what we have learned today.  This leads us to the Sandwich theorem, also known as the Squeeze theorem.

If you have three functions, f(x), h(x), and g(x), where f(x)≤g(x)≤h(x) on some open interval containing c (a range of x-values that contain endpoints) and in addition,  and  both equal L, then  MUST be L.  A picture speaks a thousand words O'Brien says, as he proceeds to draw a masterpiece that explains the Sandwich theorem.

You can use this theorem to find a function that is sandwiched between two other functions. An example is when you have , , , where .  Since the limits of the functions are all the same, we can graph these functions.  Note that f(x) is in red while h(x) is in blue.  This gives us the graph:

When we graph g(x) in green, we see that it is "sandwiched" between f(x) and h(x).

The key to this theorem is that you must know the limit of the two sandwiching functions, since their limit is the limit of the function that has been sandwiched.  If you want some more visuals on the sandwich theorem, check out this fun applet as well as this even more fun applet!

UPDATE: 

Tonight's IW (66/31, 33, 65, 72, 77) will focus on the newly learned Sandwich Theorem, where we will get to practice using it.

FUN FACT: Math team has it's first practice this wednesday, september 12th. The schedule is located here: http://math-ob.wikispaces.com/mathteam. The meeting is in O'Briens room. However, extra credit is iffy at the moment. However, some other benefits include bragging rights, great camaraderie, fun bus rides, and Ms. Orhon's and Mr. O'Brien's company.