Okay guys, time to start the painful and slightly awkward scribe post seeing as I won't be in your class when you're criticizing it. Also I apologize in advance for any errors, especially grammatical errors, which I guarantee, there will be some.
Starting off class today I walked in late with a plate full of pumpkin chocolate chip cookies and suddenly, everyone was my best friend. Even O'B said he'd give me extra credit, and yes, I'm going to hold you to that O'Brien. Then we started our warm-up which can be found
here, along with IW#7, #7's solutions, IW#8, and #8's solutions. We worked on the warm-up either alone or with a partner for a while and while we were doing this both Francie and Noah also brought in food. It's easy to say we were a happy class today. Francie brought in quinoa burgers and offered one to everyone, and even asked O'Brien directly if he wanted one but he shut her down. That was kind of harsh of him. And then not too much later Noah walked in with a plate full of peanut butter chocolate chip cookies and offered some to everyone as well. By this time we had already spent about 30 minutes of class working on our warm-up and chowing down on food.
So now onto some real math (instead of food):
Here's a quick summary of everything we did in class today:
1. Warm-up on continuous and discontinuous function
2. went over quiz #3, were reminded we have a
test on Monday, and IW#8 was handed out
3. went over the questions in IW#7 we didn't get to on Wednesday
4. took notes and learned new ways to find the derivative of a function
Starting with the warm-up . . .
1. Plot the graph of f for k=1.
The discontinuity seen at x=2 is a jump discontinuity, or a non-removable discontinuity when k=1 (definitions of both of these can be found in Lexi's scribe post
here.) As we learned earlier this year, for a function to be continuous at a point not only must the right-hand limit and left-hand limit be the same to ensure that the limit does, in fact, exist, but the limit and the y-value, in this instance
f(2), must also be the same.
Due to this discontinuity we then looked at the left- and right-hand limits as x approaches 2. But when we're looking at when x approaches 2 positively we must look at the limit in terms of
k:
*NOTE: both of the above equations should have an "f(x)" before the equals sign. My bad*
For us to make f(x) a continuous function we must make the left- and right-hand limits the same. To do so we have to find the value of k and to do that we can set the two limits equal to each other.
Now that we know that for this function to be continuous k=1/3 we can sketch the new graph:
with this new graph we can find a single limit as x approaches 2 and by looking at the graph we can see:
We can also see that the new graph has a cusp at x=2. A cusp, for those of you that don't know, comes from the latin
cuspis which means "a point or apex," and cusp's mathematical definition is: a point where two branches of a curve meet, end, and are tangent. By looking at the graph at the point (2,3) we can see that cusp is a very fitting word to use in this context. Although this cusp means that this function is still not locally linear at x=2.
Once we finished defining and talking about what a fine word cusp is we learned a couple helpful GeoGebra keyboard shortcuts, such as:
-
command -
drag to zoom in on a specified area of your graph
and -
command "
m" to return you to the standard view
We then moved onto talking about and reviewing the quiz.
The big thing we learned today while going over the quiz was all about this wonderfully useful limit called the
Golden Limit:
and how to use our knowledge of it to solve problems like 2 through 4 in our quiz.
In question #1 we mainly had to rely on our knowledge of factoring polynomials, if you could do that than you would be able to find a limit of 8.
Questions 2-4 got a bit trickier as we had to use our knowledge of the golden limit. In question #2 we had to find the limit of:
First we tried just plugging 0 in as x in our equation and we ended up with 0/0 which means this is an indeterminate function and we therefore can use L'Hospital's Rule. L'Hospital's Rule is explained
here, along with how the golden rule can be proved. Down to it's simplest form L'Hospital's Rule is find the limit of an indeterminate function as the ration of the slopes. By using L'Hospital's Rule and by just looking at the slopes of the numerator and denominator we can find the limit of this function is 3/7. This is shown below:
first we take the original equation:

then we let
by letting this be true we can manipulate the original function to try to get it to a form of the golden limit. Before we do that we must first make that applicable to all of the function by multiplying it by a FUFOO: 3/3
by doing this the equation now becomes:
and seeing as the golden rule states that
sin(x)/x=1 we have now proved that the limit of this function is 3/7.
A similar approach is used to solve question #3.
Question #4, on the other hand, had an interesting and useful way to solve it. The question asked:
Find the limit:
Since we are looking at the "end behavior" of this function (as x approaches infinity) we only have to look at the highest powers because as we get closer to infinity the limit is determined by the higher powers because they overpower values like
3x and
+1. Once we are left with only the highest powers of the numerator and denominator we get a slope of
-5/2 and a limit of
-5/2.
We quickly went over questions 5 through 8 which both mainly reviewed the rules of limits, continuity, and discontinuity. Then we took a look at the bonus and we learned that whenever you're unsure how to approach a question,
use a conjugate, it's the easiest way to get yourself started on a problem.
Once we finished going over the quiz and answering any questions on it we moved onto IW#7 and went over our solutions. O'Brien explained the intermediate value theorem by saying "if you evaluate a little above and a little below the value you're looking for it's nice because you know your answer is in between there somewhere." While reviewing IW#7 we spent most of our time looking at question 4 which asked us to find the limit of a function graphically, numerically, and algebraically.
When we first looked at this question we noticed that both the numerator and the denominator have a slope of zero, when we zoomed in close enough both of the graphs flat lined (as seen in the graph below), meaning we can't use the slopes to find the limit.
Although, when we only expanded the y-axis we began to see a difference between the two graphs, the numerator's and denominator's. By expanding the y-axis we are able to look at the
slopes of the slopes.
By looking at the above graph we can see that the blue line, the denominator, approaches zero twice as fast as the red line, the numerator. In other words, we can find the limit by looking at the ratio of the red line's y-values to the blue line's values and we get a ratio of
1/2 for the limit.
We then looked at the same function and tried to solve it algebraically, this solution is shown below. To find the limit of this function algebraically we used our knowledge of conjugates, trig identities, and the golden limit. And, as you can see, we ended up with the same answer as the limit,
1/2.
After we solved this we skipped over 5, 6, and 7 seeing as we went over them last class and went on to question 8 in which we looked at the
instantaneous rate of change. This is where the derivative of a function differs from its slope because the
derivative is the
instantaneous rate of change while the
slope is the
average rate of change. Question 8 asks to us find the slope between the points
x=0 and
x=2 for the function
g(x) and to find the derivative at both those points. The math for this problem is shown below.
*NOTE: another my bad - the last equation should "= 5" not "= lim5"*
*NOTE: last thing - in all the above equations having to do with when x=0 the limit should be when x is approaching 0, not 2, sorry!*
This method of finding the derivative, by finding the change in y over the change in x can be notationally written as either
dy/dx or
g'(2) and can be used to find every limit.
After we were taught this was to find a derivative we took a look at all five ways:
How to find a Derivative:
1. function explained above: use the function below to find the limit as x approaches c:
2. local linearity - examples in questions 3 and 5 of IW#7
3. nDeriv on our calculators - go to MATH #8 and you'll get the nDeriv option, click enter and then enter in (function, x, point) to get the derivative - this is better explained in
this video along with the option to use the #1's function on our calculators
4. Wolframalpha
5. GeoGebra
Here's an
extra site with a bunch of helpful videos explaining L'Hospital's Rule, Indeterminate forms. She rambles a bit but overall she cleared a few confusing parts up for me. Or
this video, which also explains L'Hospital's Rule, indeterminate forms, derivative, and limits pretty well. The second link also has more videos to the left explaining and proving some of the things we've gone over already and might be helpful to some in clearing up past confusions!
At the end of class we received IW#8 which is basically just a practice test and then we have
A TEST ON MONDAY, so don't forget!
And the next scribe will be....Connor! Have fun Connor :)
***UPDATE***
Since my scribe post we have learned many new ways to find the derivative of a function, such as the power rule, the product rule and the quotient rule all shown below:
The Power Rule:
The Product Rule:
The Quotient Rule:
Although I know many people are still having problems finding the derivative using the h --> 0 approach so here's another
helpful link that shows you a step by step process for varying difficulties of functions.
And another
helpful link explaining the derivatives of the trig functions because, I don't know about everyone else, but I was still having some trouble understanding how we got the derivatives.












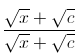








































.gif)


