Verbal:
The derivative is the slope of the tangent line. Use local linearity to find the tangent line. The slope is a rate of change. The derivative is also known as instantaneous rate of change, it is the speed at that instant. Any quantity per quantity is a rate of change: cm^3/min, $ spent/year. Anything that is changing is calculus. Calculus: the ultimate applicable mathematics.
Numeric:
See question 4 from the test. The derivative is the slope of a set of points that are really really close to each other. To do this take a set of data such as:
Now you use
and sub in each value for x-final and x-initial where x-initial is 1 and x-final is 1.0001. This gives

m=6 so the derivative is 6.
This process is called the difference quotient, aka the slope.
The symmetric difference quotient takes just a little bit above and just a little bit below x when you wish to find f'(x) of function f(x). Use
Graphing calculators can do this for you in a much simpler way by using nDeriv. It can be found by hitting math --> 8. Make sure you are not using MathPrint otherwise it is confusing. There are 4 things which need to be defined: the function, variable, the value for the variable, and some small number h. If nothing is entered for h then the default for h is 0.001
nDeriv(f(x)* ,x, 2, 0.0001)
*on your calculator use y1 from the YVARS menu.
Graphic:
take the graph of the function f(x) in this case:
Add the point (2, f(2)) which is point A then use the add point tool and make a random point on the graph so that it can be dragged around this is point B. Next put a line between these two points. This line is called a secant line.
Drag B so that it is on top of A which is supposed to give the tangent line at point A. The problem is that this is undefined 0/0, fortunately we have been learning about limits for a month! In this case to find the tangent line of A* we write our own limit:
*remember that A is really (2,4)
This gives us the slope of the tangent line which is the derivative at point A. Now we get to the more interesting part: we realize that there is a derivative for every point of f(x). We need to figure out how to find this function which gives the derivative for every point of f(x). This is incredibly easy on Geogebra, in the bottom text box you simply write f'(x) after you have graphed f(x). Unfortunately, I'm doubtful that we will be allowed to use this on opportunity days, there is an algebraic way. Before we get to that look at the graph of the derivative function (the blue line):
It is possible to have f'(x) traced by a point by entering (x(B), b) into geogebra. Where B is the point which can be dragged and b is the slope of the tangent line to B. b can be found by typing slo and selecting Slope[ <Line> ].
Algebraic:
We've done the hard work while learning about limits, the theoretical underpinning of integrals and derivatives. Find the derivative of

It is not possible to simply sub in because of the removable discontinuity. Multiply by the conjugate FUFOO of the numerator. Also, this is (above) is the definition of a derivative. PatrickJMT has a helpful video
Which gives:
The (x-c)s cancel
A general thing to know for the function f(x) at x is:
Another way to look at question 16 from the test is
So,

In part of problem 16 we were looking for when x=2. If it is plugged into the derivative the answer is

IW 1
p. 105/7, 9, 13-17, 25, 26, 27, 37
Scribe is Cooper
UPDATE:
There are much easier ways to derive functions. These ways include the power rule, quotient rule, and product rule.
The power rule:
This is extremely useful when deriving polynomial functions.The quotient rule:
Supposed there are two functions u and v so that
Once you have put in the correct values simplifying is not even necessary! Although it is recommended that we become used to simplifying this so that we improve our algebra and do better on the AP test.
The product rule:
Similar to the quotient rule because there are two functions joined together. Still using functions u and v.
Again, it is not necessary to simplify beyond this but we should become used to it because the multiple choice part of the AP test will not leave the possible answers as "messy" this, according to OB.
These ways of taking the derivative of the function are much easier than solving a limit to figure out the derivative.








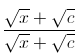
















The pictures are really inconsistent. I'm not sure what is going on there.
ReplyDelete