31-1-13 Definite Integrals, Riemann Sums, and Trapezoids

31st January, 2013

Class began today with 2 Explorations: "1-3 Introduction to Definite Integrals" and "1-4 Definite Integrals by Trapezoidal Rule," how fun.  If you want another copy, they can be found here Explorations 1-3/1-4 After doing our best to complete these explorations on our own, we went over the answers.

The 1st problem :

We basically just reviewed what we knew about Riemann Sums from the last class. To find how far you travel in the time interval [30, 50], it’s just a matter of finding the areas of rectangles. So, we simply multiply 20 (rate) by 60 (time) to find an area of 1,200 ft, which is how many feet traveled. Or, you could simply count up all the squares, and multiply that number (24) by the area of 1 of the squares (50) to get the same answer. With Riemann sums all we’re doing is adding up rectangles where the height of the rectangle is the velocity, v(t), and the base is change in time, d(t).

We then touched upon how if there is an unvarying rate of change, we can use base x height to get the area, but if there is a varying rate of change, we have to estimate to get the distance traveled. This is where definite integrals come in. We will use those later on in the football problem later.

First we discussed what exactly we need for a definite integral sum:
1. An a & b which are called the limits of integration
2. A  f(x)dx which is basically v(t)
3. A height/base

Or if you want something a little simpler : 

“In words: The definite integral sum is the limit of the Riemann sums as the number of subdivisions gets larger and larger.”

Here's a little visual representation :

Now onto the football problem :
For this problem it can be helpful to think about the football like this : [insert image here]. We have to add up all the squares, which ends up being around 230-ish. Then we have to sum up cross sectional areas to find out how much area is inside the football. Basically, the definite integral represents the volume of the football in inches cubed . It allows us to multiply the base with a variable height, how handy since footballs are not shaped like rectangular prisms. 

We then had some questions pop up:

Weston asked, “Why is it d(t) and not t ?” O’Brien said to consult his handy applet (which can be found here applet) to show that it isn’t height x time, it’s height x the change in time (velocity x change in time).

Alex also had a question concerning the units for the previous problem, something along the lines of “How is it ft?” O’Brien then showed how since velocity (ft/sec) x time (sec), it cancels out to be just ft. (Reminder that the football problem is in INCHES not FEET, otherwise that would be a pretty massive football).

O’Brien then took the time to tell us to calm down about the definite integrals.
“Just breathe with our definite integral!” He said gleefully.
The class was not amused.

...moving on...


Besides those pesky Definite Integrals we also were introduced to something even more ridiculous:  Trapezoids.

More specifically, this mess (let's try to ignore the terrible attempt at a Star Wars pun) :

Anywhoozies...trapezoids, why? Well, a trapezoid has fewer error than our Riemann sum rectangles because rectangles have 2 of the same points. To find the area of a trapezoid we have to average the bases, then multiply by height : 




So by adding up all our trapezoids we are going to get a more exact definite integral. Exactly what we always wanted! What makes this that much better is that we can use Geogebra to model this for us. Using the velocity function from the problem :

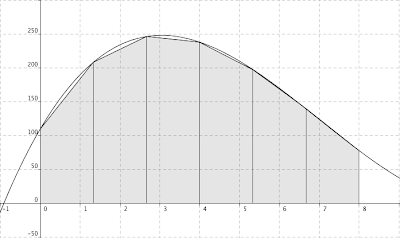
We simply graph that function like normal, then type “trap” and fill in all the areas. It should look like this:

Then, if you wanna get really fancy, you can set n to be a slider, so you can adjust the number of trapezoids to get a more or less accurate area. You should get something like this :

Oodles more accurate than those rectangles.

Some more tech tips were then brought up.
To do definite integrals on your calculator : fnInt
For Geogebra : type “integral” and plug in your function starting/ending points and you get your area integral. yay.

We then had a brief intermission from all this madness when OB went about pulling his awkward potted tree across the room on a string. Yes, this is our AP Calculus teacher.

Once the tree had been returned to its rightful place in the corner of the room we continued with class as usual. Jumping back to those Riemann Sums (rectangles, not trapezoids) we learned that when we’re approximating definite integrals with Riemann Sums, we get 5 different choices of Rectangular Approximation Method (RAM). They are :
LRAM — “L” for left [0]
RRAM — “R” for right [1]
MRAM — “M” for middle [.5]
Upper RAM
Lower RAM

The way we use these on the ever-powerful Geogebra (for the first 3): type in rectangular sum and plug in the all the values except for “Position for rectangle start”. Then, depending on which RAM you’re doing you plug in either 0, .5, or 1. LRAM is 0, RRAM is 1, MRAM is .5. However, if you’re trying to use Upper/Lower RAM you simply type in upper sum or lower sum. Easy peasy.

Now let's have some visuals :

LRAM

MRAM

RRAM

LOWER

UPPER

And lastly we got dealt this crazy-looking thing :

[The interval [2,1] is partitioned (yes, I spelled partitioned wrong in the above photo, I'm tired) into "n' subintervals of depth ∆x = 3/n let x sub 3 denote a point in the k^(th) subinterval]


Apparently though, if the change in x is 3/n then 3 is coming from the length of the partition interval. You can separate ∆x as the base and the stuff in parentheses as the height, and from there you can just plug that into your calculator as

That's all for now. Final thoughts from the class :

Autumn : why can’t this class be over?

Noah : O'Brien hates us all.


IW #7
The supercorrections for our Free Response Question Quiz and...
p. 274/5, 23, 31, 35
p. 286/3, 7, 13, 19, 43, 45
p. 318/31, 35



[STILL IN THE PROCESS OF EDITING. DON'T JUDGE ME]

Reimann Sums- Cooper Krause Jan 29th

Cooper Krause
January 29th, 2013

We started class with a quiz that we will be getting back and possibly super correcting today. Then... the learning began.

We started by referring back to the question Mr. OB asked us last class.

True or False: An object that has a negative acceleration is slowing down.
If I remember correctly, 7 of us answered the correct answer of true, and 4 answered the incorrect answer of false. A ratio of slightly above 50% of the class got the question correct. Decent job guys, decent job.

The answer is false because: when an object has a negative acceleration, it means the velocity is decreasing. If the velocity is positive and decreasing, then the speed is decreasing. However, if the object has a negative velocity and a negative acceleration than the speed is actually increasing in the negative direction. The key to what we have been talking about the last few days is that speed does not take direction, whether it be positive or negative, into account. In other words that have been repeated many times recently, speed is the absolute value of velocity.

To solidify the ideas of speed, velocity and acceleration and how they are related we went over IW #5 which asked generalized questions about the topics.
Things to Remember:
-When the speed is increasing the velocity and acceleration have the same signs.
-When the speed is decreasing, the velocity and acceleration have opposite signs.
-Acceleration is the derivative of velocity
-Velocity is the derivative of position

Next we started  PART 2 OF CALCULUS with Reimann Sums.


We started by using the concept velocity X time = distance to complete the Reimann sum worksheet. We found that Reimann sums are used to estimate the max and min distance traveled when we know know certain speeds at certain times.




To reach our minimum value for example we assumed that the velocity remained at 30 ft/sec for the first 2 seconds and then at t=2 instantaneously switched to the new assigned value. For the maximum value we assumed that the velocity instantaneously went to 36 after t=0 and so on. We found that if we double the amount of segments where a velocity is assigned, so every one second instead of 2, no matter what we assigned for the new velocity values the error between the max and min sums was always the same. The error was also half of the original error when we doubled the amount of segments.

This picture as a graphical analysis of an upper and lower Reimann Sum. The upper Reimann sum includes the blue rectangle at the top as well as the red which is representative of the lower Reimann sum. The blue box itself represents the error between the two Reimann sums.
This final picture shows a plausible function connecting the original velocity/time coordinates assigned: A, B, C, D, E and F. This plausible function sets down an amount of segments that approaches infinity. There is no difference between the max and min Reimann sums. This area is known as the definite integral.

That's pretty much where we ended guys. Have fun with IW #6 and super corrections. I know you willll!!!!!!!!

1.25.13

1.25.13

We began by putting IW#4, arguably the easiest IW to date, on our desks to begin class. OB had the class look at the answers via computer, and then led the class in a rousing discussion about the IW.

We noted the use of the I.V.T when looking at when the particle is at rest in question 2, on example 1 of the IW. This is the kind of calculus reasoning we can use of the AP test.

Using fitPoly in Geogebra you can take a table as seen in example 1 and make a list of points and draw a function through all of them to show you what type of polynomial the function is. 

However, some of the time you wont have the entire function and you just have the values from the table. Then finding the slope can be done by finding acceleration, given a v(t) chart, since a(t) is v’(t).

For number 3 on the IW, Noah remembered the Symmetric Difference Quotient, which is just nDeriv. Taking a point on either side and calculating the slope off the line from point to point. OB pointed out than units for acceleration come from the fact that  which gives you units of , Which is . So in terms of motion, if the acceleration -1/2, the particle is slowing down at that point.

Using a graph we can see 4 places where the graph changes from increasing to decreasing, meaning there is 4 places where acceleration is zero, since acceleration is the derivative of velocity. 

OB asked if a function is differentiable, must its derivative be differentiable. He shockingly answered “no”. He said there was extra credit for everyone except Eliot if they found an example of this. 

The second page had little confusion and the answers can be seen on the Even Answers page of the blog. Its's important to note that a table only gets us so far OB says, you have to look at an instant in time to really tell.

SURPRISE! Quiz tuesday! YAAAAY! What a treat!

LEAP FROG TIME. SOLIDIFY THOSE BASICS. BLOW MINDS. LEAP FROGS. IW#5. CONFUSION. SPEED.

The goal for the leap frog game is to make us leave confused about speed. I suppose it was successful, since the game was quite easy in general, and then only questions people seemed to be confused on were when it asked about speed instead of velocity.

January 23, 2013

We started out class by talking about how to get a 5 on the AP test this may. Really all you need to get is 30 points on the FRQ. For the free response question, you have 90 minutes to answer 6 questions, which averages to 15 minutes per question. Nine points are allocated for very specific things. 

We worked on questions D and C from the midterm exam, starting with question D, which was fairly straightforward in its processing and grading: 

To solve for part a, you could receive points for the following:

 For part b, you could receive points for the following:

And finally, for part c, you could receive points for the following:

 We then went on to work on part C, which was more tricky in understanding what was expected in your answer. The question is posted below:

We started by analyzing what we know about the functions. Function f is a quadratic function, function g is a cubic, and function h is a power function. What determines that function h is a power function is the variables location in the base, not the power. Power functions are fairly easy to solve, like a cubic or a quartic, and you can use the power rules to find the derivative. To answer part a, there were a couple of ways to show that it is not possible to find a value for a so that f meets the second requirement. One way to solve this is shown below:

 The points in this problem are allocated for doing some sort of calculation to find a value of a, and some calculation to show that it does not work for another qualification. To solve part b, you need to find a value for c to receive the point.

 In part c, the best way to go about this problem is to look at the critical points, because that is where the derivative changes signs. Using some calculus you can find the derivative, shown below. 

 An important piece of information here is in the explanation. On these free response questions it is really important to justify your answers with calculus. Use of language is very important. Saying something like "the function" or "it" won't be accepted, because it is too ambiguous and could refer to anything. You have to be careful to check over your sentences and justifications to avoid ambiguity, and make sure to use calculus to prove your answer is correct!

Finally, in part d, four points were available. To solve, you need to take the function and evaluate it at four, but also take the derivative at four and set that equal to one. Using the power rule, you can get a system of equations: two equations with two variables. This can be solved with the graphing calculator or using substitution to find n=4. Then you can solve for k with your n value of 4 and get 256. Points are given not only for finding values  and setting the equations equal to one, but also in verifying your answers (h(0)=0, h'(0)=0, and h'>0 for 0 < x < 4). This is given below:

 If you're worried about these FRQs, don't be! Over the next few months we will be doing a lot of these problems to prepare for the test.

After going over the midterm free response questions, we went over the answers to the multiple choice questions. The multiple choice can't be released, so we won't go over that, but if you have questions about how to solve the problems I'm sure Mr. O'Brien would allow you to come in for help.

To finish off class, we started looking at a more physics oriented side of calculus. In unit four, we're taking time to go back and look at motion, including but not limited to position, velocity, displacement, distance, and acceleration. For this unit, it's important to know the physics students so that the class can make sure who to ask for help and also be aware of those in the class that have never seen this sort of problem before.

There are a few definitions that may be found helpful at this point. Position, x(t) or s(t), is the location of a particle at time t. Velocity, v(t)=s'(t), is how fast the position is changing. Acceleration, a(t)=v'(t)=s''(t), is how fast the velocity is changing. 

We did a fairly confusing exercise where Eliot and Connor  were particles, and Mr. O'Brien posed several questions that were more confusing then elucidating. What we did determine was at time 0, the position of Eliot was x(0)=7. For Connor at time 5, the position of Connor was x(5)=-4. Position is a particular number representing a particular place in a line, relative to the point, either to the right or left of the origin. We determined that distance divided by time is equal to average speed, or velocity. The average speed in this case is 11/5, which is also the velocity. However if Eliot moved around before moving towards Connor, it doesn't make sense to take the distance and divide it by the time, because we're not talking about a moment in time. We then started to talk about displacement which is the amount by which a thing is moved from its normal position. We tossed around the idea of whether the displacement of Eliot to Connor is any different from the displacement of Connor to Eliot, and determined that the displacement from Eliot to Connor is -11, while from Connor to Eliot it is 11. This is because Connor is moving in a positive direction while Eliot is moving in a negative direction. Finally, we answered the question of whether the velocity is different from the average speed of Eliot moving to Connor. The average velocity of Eliot moving to Connor is thus -11/5, while the average speed is in fact 11/5.

We finished up class with a few minutes to work on 11 questions from the link on iCal. The answers are posted here:

http://ssh.springbranchisd.com/LinkClick.aspx?fileticket=cm531BaGtCw%3D&tabid=17567&mid=78702


Due for Thursday: 11 questions
Due for Friday: IW#1
There will be no extension for IW#1 past Friday.

Midterm Answer Sheet

Midterm Answer Sheet

Jan. 9 Links

IW #3 Classwork problems

Scribe Post 1/8/12

Mr. O’Brien began class today by introducing us to Ms. Nightingale aka Stacy aka Marc Belléy’s mom! She’ll be student teaching with O’B for a few weeks. Yes!

Today’s class was dedicated to integrals. We continued going over IW #1, focusing on problems 17 and 18. First, we looked at the basic form of differential equations and integral equations. A differential equation is usually formed in this way:
In order to get an integral, you have to separate the variables like this and add a funky symbol called an integral sign. The general form of an integral is:
There are three components to an integral equation – the integral sign, the integrand and the differential.
Basically all these confusing symbols and letters mean “take the antiderivative of” whatever is inside the integral sign! That’s not too hard.

Now we got onto working on the IW questions. This equation:  was given for number 17. Our job was to find the particular solution  to the equation with the initial condition . We simplified the equation to make it easier to change forms. The new equation looked like this: . In order to get an answer, this differential equation has to be changed into an integral equation. The work for the problem is like this:
When taking the antiderivative, there are some things that you need to be aware of! The natural log trick doesn’t always work...sometimes there are nasty chain rules that have to be accounted for. Here’s an example of one! Imagine you had this integral:
Naïve thinking could lead someone to think that they could just use the natural log to find the antiderivative. However, there’s a sneaky chain rule! In order to find the antiderivative you have to do this:
Getting back to the IW work, we had to compare our estimate of to the actual answer. But what exactly was our estimate and how did we find it? We had to find the linearization of the differential equation using a point and a slope. The point was given to use, and we could easily find the slope by plugging values into the equation.

When comparing our estimate and the real answer, we found that we underestimated! Thinking back to the old Finely Crafted Opportunity Day, we know that we had a question similar to this one. (Look back at question 10). We know that the function must be concave up at the point (1,1), and if you look at the slope field, it is! O’B showed everyone Eliot’s slope field, which he thought was beautiful.

We quickly moved onto question 18 from the IW. O’B pointed out that the function given by the differential equation differs depending on which “root” you look at. For example, at , the function will be different than at . You also can’t use both points at the same time because the differential equation will no longer be a function! The first step to solving number 18 is turning the differential equation into an integral. That can be done like this:
Notice the trick we used! Because C is only a constant, it can be any number at all. Therefore you can simply get rid of the coefficient of 2. It’s a different number, but it’s still a constant! Tricky... Carrying on from there we can find a particular solution at .







After coming to that conclusion, Sarah Mayberry asked why part E wouldn’t have the exact same answer. O’B, of course, thought this was an excellent question, so we worked it out on the board, which was incredibly messy and hard to read.





Although it was close to being the same answer, there was a sneaky negative sign out in front of the square root symbol! Darn.
As soon as we finished going over IW questions, Mr. O’Brien passed out a double-sided exploration. At first glance, everyone was immediately stuck. That’s when the groaning and sass began. Sarah Mayberry shouted out: “O’BRIEN! THROW US A BONE.” Reluctantly,he did. He told us to write the problem out in words to see if that helped. Here’s what was on the board:
Autumn immediately began complaining about the use of “K” as a constant by saying: “BE CONSTANT WITH YOUR CONSTANTS!” Also, a side note, as we were working on the explorations, O’B handed back supercorrections to certain people. He basically said that if you got them back then you suck aka “you’re not a respectable student” aka YOU’RE SASSY. Anyway, after “throwing us a bone”, we all continued simplifying the differential equation like this:




Now, there’s a trick to simplify even more. Thinking back to freshman or sophomore year, we remember a power rule that goes like this: . This rule can be applied to the equation above.

Mr. O’Brien reminded us of a familiar equation, . That equation looks familiar because it was used in a project last year! Hmm... If you think about it, the expression of  will always be positive because power functions are always positive! You can replace  with the new constant  because the constant accounts for the change of sign. The new equation is now:

At this point, we finished all the actual calculus for this exploration. YES! The rest is all algebra. For question 6, we had a money amount of $1000. Solving for , you should get something like this.



If the interest rate is 5% per year, then  which means that .

To find out how long it takes for the amount of money to double its initial value, you simply double the initial value in the initial equation:



 

Yes! We finally finished an exploration...but wait. There was another. This exploration was about memory retention and how Ira Member has a serious mental issue. After an in-depth discussion of how screwed up Ira might be, we actually got onto working. To read up more on how people remember, read this simple explanation from eHow. Anyway! Onto more math. Mr. O’Brien let us know that identifying variables is super important, otherwise everything is just “alphabet soup”. So here are the variables for this problem:

He also pointed this out:

People pointed out that O’B was doing a lot of assuming for this problem, and you know what they say about assuming! We finally got on to determining our integral function!






The only variables we care about in the equation above are  and . We know that the absolute value sign in front of  can be taken away. That value is always positive because the rate which Ira forgets is always smaller than the rate at which he meets people. In order to evaluate the value of  at , you simply plug that into the equation we found to get:


In question 6, we suppose that Ira meets 100 people per hour, forgets at a rate of 4 names per hour and  names. The particular equation could then be found like this:


When that equation is graphed it looks like this:

*This graph is incorrect! When first done out in class, we supposed the value was , not like it should have been.

To find out how many names Ira will have remembered at  hours, you simply plug 3 into the equation above.

Here’s a lovely PatrickJMT video on solving differential equations, as well as a website talking about them as well! Hopefully after all these examples, everyone will understand them super well.

The IW for next class is the IW #2 packet!