Today’s class was dedicated to integrals. We continued going over IW #1, focusing on problems 17 and 18. First, we looked at the basic form of differential equations and integral equations. A differential equation is usually formed in this way:
In order to get an integral, you have to separate the variables like this and add a funky symbol called an integral sign. The general form of an integral is:
There are three components to an integral equation – the integral sign, the integrand and the differential.
Basically all these confusing symbols and letters mean “take the antiderivative of” whatever is inside the integral sign! That’s not too hard.
Now we got onto working on the IW questions. This equation:
was given for number 17. Our job was to find the particular solution 
to the equation with the initial condition 
. We simplified the equation to make it easier to change forms. The new equation looked like this: 
. In order to get an answer, this differential equation has to be changed into an integral equation. The work for the problem is like this:
When taking the antiderivative, there are some things that you need to be aware of! The natural log trick doesn’t always work...sometimes there are nasty chain rules that have to be accounted for. Here’s an example of one! Imagine you had this integral:
Naïve thinking could lead someone to think that they could just use the natural log to find the antiderivative. However, there’s a sneaky chain rule! In order to find the antiderivative you have to do this:
Getting back to the IW work, we had to compare our estimate of
to the actual answer. But what exactly was our estimate and how did we find it? We had to find the linearization of the differential equation using a point and a slope. The point was given to use, and we could easily find the slope by plugging values into the equation. 
When comparing our estimate and the real answer, we found that we underestimated! Thinking back to the old Finely Crafted Opportunity Day, we know that we had a question similar to this one. (Look back at question 10). We know that the function must be concave up at the point (1,1), and if you look at the slope field, it is! O’B showed everyone Eliot’s slope field, which he thought was beautiful.
We quickly moved onto question 18 from the IW. O’B pointed out that the function given by the differential equation
differs depending on which “root” you look at. For example, at 
, the function will be different than at 
. You also can’t use both points at the same time because the differential equation will no longer be a function! The first step to solving number 18 is turning the differential equation into an integral. That can be done like this: 
Notice the trick we used! Because C is only a constant, it can be any number at all. Therefore you can simply get rid of the coefficient of 2. It’s a different number, but it’s still a constant! Tricky... Carrying on from there we can find a particular solution at
. 
After coming to that conclusion, Sarah Mayberry asked why part E wouldn’t have the exact same answer. O’B, of course, thought this was an excellent question, so we worked it out on the board, which was incredibly messy and hard to read.
Although it was close to being the same answer, there was a sneaky negative sign out in front of the square root symbol! Darn.
As soon as we finished going over IW questions, Mr. O’Brien passed out a double-sided exploration. At first glance, everyone was immediately stuck. That’s when the groaning and sass began. Sarah Mayberry shouted out: “O’BRIEN! THROW US A BONE.” Reluctantly,he did. He told us to write the problem out in words to see if that helped. Here’s what was on the board:
Autumn immediately began complaining about the use of “K” as a constant by saying: “BE CONSTANT WITH YOUR CONSTANTS!” Also, a side note, as we were working on the explorations, O’B handed back supercorrections to certain people. He basically said that if you got them back then you suck aka “you’re not a respectable student” aka YOU’RE SASSY. Anyway, after “throwing us a bone”, we all continued simplifying the differential equation like this:
Now, there’s a trick to simplify even more. Thinking back to freshman or sophomore year, we remember a power rule that goes like this:
. This rule can be applied to the equation above. 
Mr. O’Brien reminded us of a familiar equation,
. That equation looks familiar because it was used in a project last year! Hmm... If you think about it, the expression of 
will always be positive because power functions are always positive! You can replace 
with the new constant 
because the constant accounts for the change of sign. The new equation is now:
At this point, we finished all the actual calculus for this exploration. YES! The rest is all algebra. For question 6, we had a money amount of $1000. Solving for
, you should get something like this. 
If the interest rate is 5% per year, then
which means that 
. 
Yes! We finally finished an exploration...but wait. There was another. This exploration was about memory retention and how Ira Member has a serious mental issue. After an in-depth discussion of how screwed up Ira might be, we actually got onto working. To read up more on how people remember, read this simple explanation from eHow. Anyway! Onto more math. Mr. O’Brien let us know that identifying variables is super important, otherwise everything is just “alphabet soup”. So here are the variables for this problem:
He also pointed this out:
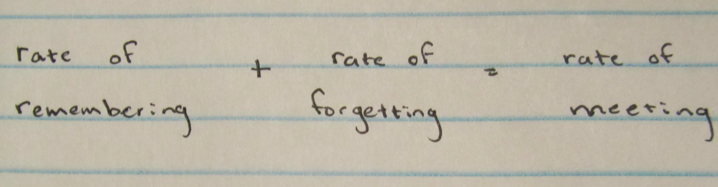People pointed out that O’B was doing a lot of assuming for this problem, and you know what they say about assuming! We finally got on to determining our integral function!
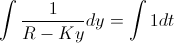
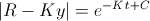
The only variables we care about in the equation above are
and 
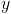. We know that the absolute value sign in front of 
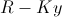can be taken away. That value is always positive because the rate which Ira forgets is always smaller than the rate at which he meets people. In order to evaluate the value of 
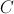at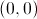 
, you simply plug that into the equation we found to get:
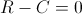
In question 6, we suppose that Ira meets 100 people per hour, forgets at a rate of 4 names per hour and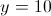
names. The particular equation could then be found like this:
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
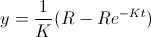
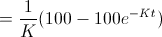
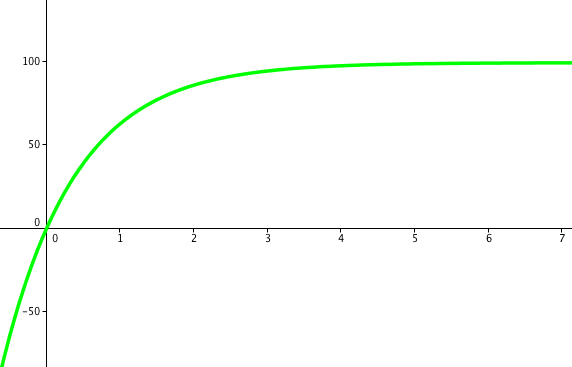
When that equation is graphed it looks like this:
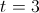hours, you simply plug 3 into the equation above.
Here’s a lovely PatrickJMT video on solving differential equations, as well as a website talking about them as well! Hopefully after all these examples, everyone will understand them super well.
The IW for next class is the IW #2 packet!
The only variables we care about in the equation above are
and . We know that the absolute value sign in front of can be taken away. That value is always positive because the rate which Ira forgets is always smaller than the rate at which he meets people. In order to evaluate the value of at , you simply plug that into the equation we found to get: In question 6, we suppose that Ira meets 100 people per hour, forgets at a rate of 4 names per hour and
names. The particular equation could then be found like this:When that equation is graphed it looks like this:
*This graph is incorrect! When first done out in class, we supposed the 
value was 
, not 
like it should have been.
To find out how many names Ira will have remembered at hours, you simply plug 3 into the equation above. Here’s a lovely PatrickJMT video on solving differential equations, as well as a website talking about them as well! Hopefully after all these examples, everyone will understand them super well.
The IW for next class is the IW #2 packet!
No comments:
Post a Comment