Link to the even answers: http://math-ob.wikispaces.com/AP+Calculus+Even+Answers
Mr. O'Brien then briefly went over each quiz problem before anyone asked any clarifying questions.
A good problem to look at was problem six (which has great potential of being on the quiz Thursday). The problem was
"Use the x --> c form of the derivative to find the derivative of

at x=5. Show appropriate working."
Three important things for successfully completing this problem were: 1. memorizing the x --> c derivative form which is shown below. 2. conjugate foofoo and 3. let c be the number you are approaching. With those three things you should be able to complete the problem easily as it is shown below:
x-->c derivative form:
.gif)
After going over problem number six on the quiz we began to move on to old IW questions but before this Mr. O'Brien made a note to tell us that MATCHING GRAPH TO DERIVATIVE will be added to the quiz on Thursday so playing the matching game will be helpful. Also to practice marginal cost, marginal revenue, velocity, and displacement problems which were on IW 5.
The first IW question we went over was problem #19 on page 136 from IW 5.
The problem was:
Particle Motion A particle moves along a line so that its position at any time t > 0 is given by the function
where s is measured in meters and t is measured in seconds.
a) Find the displacement during the first 5 seconds.
This can be easily done by first plugging 0 into the equation which gives you a position of 2m and then plugging 5 into the equation which gives you 12m. Displacement is the difference between when you started and ended so the answer is the difference between 2m and 12m which is 10m.
b) Find the average velocity during the first 5 seconds.
Average velocity is the same as the slope (derivative) so all you had to do for this part of the problem is solve for the derivative at 5.
c) Find the instantaneous velocity when t=4.
To solve for the instantaneous velocity you need to take the derivative of the given equation and then plug in the instant, in this case 4 seconds, that you are looking for.
.gif)
*Note: Pay careful attention to units on problems such as this one. It may help to write it out as
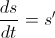.gif)
because you know from the problem that s is measured in meters and t is measured in seconds so it is m/s.
d) Find the acceleration of the particle when t=4.
Finding the acceleration is the same as finding the derivative of the velocity.
e) At what values of t does the particle change direction?
The particle changes direction when the velocity goes from positive to negative so to find the answer all you have to do is set the derivative of the function (which is the velocity) and set it equal to zero because that is the point where the particle would be going from positive to negative.
Because the x axis is time and time does not go negative the minimum value would be found at 1.5 seconds which we just found is where x=0. So to answer the question we have to plug 1.5 into the first given equation.
Next there was a question asked about #13 part D on IW 5.
The problem was:
Lunar Projectile Motion A rock thrown vertically upward from the surface of the moon at a velocity of 24m/sec (about 86 km/h) reaches a height of
.gif) meters in t seconds.
meters in t seconds.d) When did the rock reach half its maximum height?
We were able to solve this problem by making a graph of the given equation which looks like this:
 The graph shows us that the half way point is at the y value of 90 (because the y max is 180 and half of that is 90) so if you plug in the given equation as y1 on your calculator and y2 equal to 90 and then go to 2nd calc intersect to find the intersection of the two on your graph the intersection will be your answer. 4.393 seconds.
The graph shows us that the half way point is at the y value of 90 (because the y max is 180 and half of that is 90) so if you plug in the given equation as y1 on your calculator and y2 equal to 90 and then go to 2nd calc intersect to find the intersection of the two on your graph the intersection will be your answer. 4.393 seconds.The last IW question was from Weston asking about problem #27 part A because he kept getting an answer of 90 which did not add up with the back of the book. After reviewing the problem in class, we found out that the back of the book made a mistake!! and Weston's answer of $90 per machine was actually correct.
The problem was:
Marginal Cost Suppose that the dollar cost of producing x washing machines is
a) Find the average cost of producing 100 washing machines.
All you need to do for this problem is plug in y1 as
Then go to your table and plug in 100 as x which gives you a y value of 11,000 and plug in 0 as x which gives you a y value of 2,000. Then subtract the two from each other to get 9,000 and divide 9,000 by 100 which gives you your answer of $90 per machine.
Then, in order to see the derivative of this sin function we needed to follow the following steps:
1. Use the "new point" tool in Geogebra and click on a point on your function to make a point A.
2. Type "tangent" into the input box and choose the option "Tangent[ <Point>, <Function> ]" and type in A for your point and f(x) for your function. This will give you the tangent line to the point a on your sine function.
3. Then click on the slope tool in Geogebra and click on point A, then type into input (x(A), m) which will give you point b (the slope a.k.a the derivative of point A).
4. Right click on point b and turn on trace and as your point A moves it will trace out the derivative for you.
After following these steps you should have a graph that looks like this:
What does the derivative of f(x)=sin(x) appear to be according to the graph? COS(X) ..... but we all know graphs can lie, so to double check we put f(x)=cos(x) into the input box and it confirmed that (sin(x))'=cos(x)!.
We then proceeded to do this for all six trig functions by using command f to clear the current traced derivative off the graph and then plugging in our next trig function into our equation and retracing the derivative for the new trig function. Our results were as follows:
At first glance the derivative looks like just sinx but the slope from zero is negative instead of positive so the derivative is -sinx.
This derivative is secx but to get only the positive values above the x-axis you have to square secx.
This graph is similar to the one above but it needs to have a negative sign in front of the derivative because it is the negative values. Also because it is cot instead of tan the derivative is csc instead of sec.
Something helpful when trying to remember these derivatives is thinking back to last year when we were looking at trig relationships. Mr. O'Brien pointed out to us that tangent and secant commonly are associated with each other. Also cotangent and cosecant were often found associated with each other and of course sine and cosine, all of these relationships still remain true with these derivatives. Another relationship we notice is that the derivative is negative when with "co" such as cot and cos.
Because we found all these using Geogebra and we have learned in the past as stated before that graphs can lie, Mr. O'Brien had us prove some of these algebraically to make sure our answers were correct.
We first started by proving that (sinx)'=cosx. We did this using the derivative definition:
We then plugged in sinx as our function.
.gif)
This was in indeterminate form though so we needed to go further. We used the sum identity for sin from Pre-AP Calc which is
We then were able to break down our function:
We know that the limit as h approaches 0 of sin(h) over h is equal to one.
We continued to simplify the end of the equation by using a Lemma (a little theorem to prove a bigger one).
*We know that the limit as h approaches 0 of sinh over h is going to be equal to one and to solve for the second part we need to plug in 0 which simplifies to the following:
Now if we plug what we proved using the lemma into the equation we get the equation below:
And we proved it! (sinx)'=cosx!
Below are the rest of the proofs we went over in class:


QUIZ NEXT CLASS (THURSDAY OCTOBER 18, 2012) ON IW #1-#5
IW 6 - Page 146/1, 5, 7, 21, 26, 31, 43, 47, 49 and Page 148/1-4
.gif)
.gif)
.gif)
.gif)
.gif)

.gif)
.gif)
.gif)
.gif)
.gif)



.gif)
.gif)

.gif)

.gif)

.gif)

.gif)

.gif)
.gif)
.gif)
.gif)
.gif)




UPDATE:
ReplyDeleteThe following video shows an example of how to take the derivative of a trigonometric function. After the video finishes there are several links to more examples of how to use the chain rule, product rule and quotient rule. Also there are more trig function examples and even natural log derivative examples.
http://www.youtube.com/watch?v=MEoH-M6T-CI