Scribe Post 10/23

Today’s class began with an extremely unusual video. If anyone cares to watch it again, here’s the link: http://www.youtube.com/watch?v=CkdRVS-zKEQ Finally, we got on to doing some real math. Today’s warm-up had to with rubber-bands and the chain rule. Although it was supposed to make everyone really think, many people were simply having their own side conversations. After reading over the sheet, Hayley yelled, “I didn’t sign up for PHYSICS!” As the talking continued, Francie said something along the lines of, “Shut up! People are trying to work here.” This comment caused Elazar to say, “This is a hostile environment.” Finally, people were beginning to finish up their work. Was it a beneficial warm-up? Lexi didn’t think so, exclaiming, “I didn’t learn anything!” Mr. O’Brien interrupted the chaos in order to go over the answers for the work, but not before adding some O’Brien wisdom. “Take the opportunity to stretch your brain on these warm-ups. If you don’t engage yourself, you won’t get where you need to be in AP Calculus.”

First, he shared a cool little calculator trick. Using technology, you can use the 2nd PRGM (draw) button and then press the Tangent button to find the equation of a tangent line at a point. It’s a pretty cool trick, and what’s even better is that Period 2 doesn’t know it! In order for it to work, your calculator has to be on the graph screen. Another thing to keep in mind is, it only works for finding the equation of a tangent line. There’s no help for finding the same for a normal line. Here’s an example of this trick:

ex/ 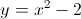     Find the equation of the tangent line at .

By graphing this equation on your calculator, you can use 2nd PRGM → Tangent at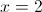

The equation of the tangent line is: 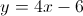! It’s that easy.

Before we started to look at the mathematical components of the warm-up, we analyzed what the different variables meant in the problem situation. The table represented a rubber band being pulled back and let go. Therefore, the x values represented the length of the rubber band. O’B pointed out that you don’t have to be a physicist to do calc! Plotting points for the graphs of x(t) and F(x) results in these two graphs:





When finding either  or  use the symmetric difference quotient, which is .  Finding  when  can be done like this:

Another way to find the answer is using either the forward difference quotient,  or the backward difference quotient, . Either approach can be used to find  when . which should give you an answer of .  By drawing tangent lines on both graphs at the indicated values, it is possible to find the slope of the tangent line, which should be the same as the answers above.
Next, we were supposed to graph  vs.  which should look like this:


The chain rule states that . Using this definition, we can find  at :  
(Notice how stoichiometry is used here! Doesn’t that bring back fond memories of chemistry?) Now, let’s see if we can get the same answer using direct data:  (again, the second values are from the symmetric difference quotient)
Geometrically, you can can use the slope of the tangent line to make sure that your answers are correct! Now, the real question is, what did you learn as a result of this warm-up?
Next on the class agenda was correcting the quiz! A simple way to answer question 1 is by using nDeriv. Otherwise, find the derivative of the function and evaluate it at . HINT HINT: Matching graphs will be on the next quiz! There are four things to look out for:
1. Maximum and minimum points
2. Zeroes!
3. When a function decreases, it’s derivative will be negative
4. When a function increased, it’s derivative will be positive

*Using power rules will not necessarily help you!*

Use the derivative matching game to brush up on your skills.

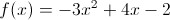For number 3, the derivative gives you a slope for the point you need, but it isn’t necessary. Using nDeriv will work just as well! Once you find the slope of the tangent line, you have to find the slope of the normal line. (Remember, the slope of the normal line is the opposite reciprocal of the tangent line). Then, plug the value of  into the equation  to find your  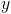value. To gain a better understanding of this, use geogebra:

In order to completely understand question 4, you have to understand the constructs velocity, speed, and acceleration. If you’re taking physics, I’m sure Mrs. Damian had drilled these into your brain. Velocity is the derivation of position, so in order to find velocity at , take the derivative of , which comes out to be , evaluating at 1 will give you the velocity which is . When getting to the second part of this problem, some conceptual knowledge on speed is needed. Speed can never be negative, so really, . Remember that we are finding speed at , not . Acceleration is the derivative of the velocity function, or in the second derivative of position. Number 5 and 6 were trickier versions of concepts that we’ve been using all year. Things to remember when doing these problems are conjugate FUFOOs and algebra errors! Be very careful!
Mr. O’Brien shared a tricky way of simplifying number 7 on the quiz. The  in the numerator and the  in the denominator cancel to be just . Then, the  reduces to be . What’s left is , which reduces to .
If you thought the bonus was easy, apparently it is.  is just asking you to take the derivative of .  
Just when you thought O’B couldn’t have packed more math into one class, he did. His new question is: Is the derivative of an odd function always an even function?
First let’s define odd vs. even:
An odd function has origin symmetry, that is:
An even function has y-axis symmetry, that is:
ex/ is an odd function ex/ is an odd function
which is an even function  which is an even function
Another example is the odd function , shown below:

The function above is an odd function, and when the trace function is used on geogebra, we can see that it’s derivative (the black trace parabola) is an even function. We also have to remember that functions don’t have to be even or odd, so it’s possible that the answer to the  question could be “no”. With this, it’s proof time!

Check out this website if the proof above is confusing to you. It’s essentially the same thing, except that it includes a lemma and uses the  method.

Remember!
QUIZ ON WEDNESDAY
IW #8 → Pink sheet from class
The next scribe will be Hayley. Have fun!

*UPDATE*

Mr. O'Brien noted that our class was particularly unfocused the day of my scribe post. Therefore, there was a little change to our 40 minute period. Instead of asking IW questions, we caught up on two problems which were we supposed to take notes on yesterday. The first problem was:

ex/ Find the equation of the tangent to a circle centered at the origin with a radius of 4 when  and  is positive. 

First, we will look at this problem geometrically:

Next, we must look at the problem algebraically, to see if the answer is the same:

We do! But, as O'B pointed out, it's much less work getting the answer geometrically. If you understand that approach more, great! It means much less work.

The next problem that we were given was finding the equation of a normal line at  with the equation . The work for this problem is as follows: